봉황대 in CS
[Chapter 3. 컴퓨터 연산] 부동소수점 덧셈과 곱셉 본문
[Chapter 3. 컴퓨터 연산] 부동소수점 덧셈과 곱셉
등 긁는 봉황대 2022. 8. 29. 16:41* 본 글은 '컴퓨터 구조 및 설계: 하드웨어/소프트웨어 인터페이스(Computer Organization and Design: The Hardware/Software Interface) 5th edition'의 내용과 2021학년도 1학기에 수강한 '컴퓨터 구조' 과목 강의 내용을 함께 정리하여 작성하였습니다.
부동소수점 덧셈
부동소수점으로 표현된 수들의 덧셈은 어떻게 진행되는지 알아보자.
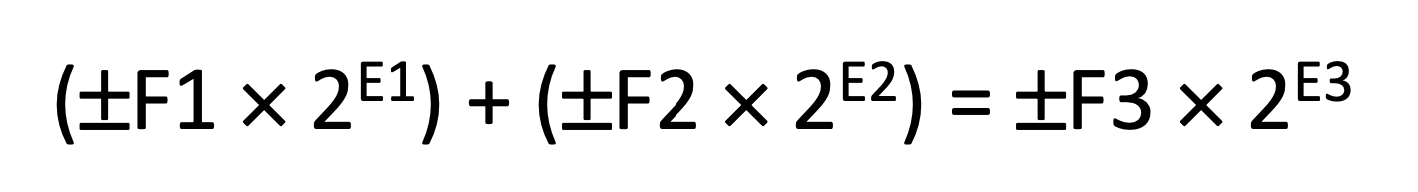
1. F1과 F2의 hidden bit을 복구시킨다.
ex) F1이 011000...000이라면 원래 수는 1.011이다. (hidden bit = 1)
2. E1과 E2의 자릿수를 맞춰준다.
* 자릿수를 맞추는 방법
(1) E1과 E2 중에 큰 것을 고른다. E1 > E2라고 가정하자.
(2) E1 - E2 만큼 F2를 right shift(나누기 2) 해준다.
(3) 만약 F2가 표현할 수 없는 비트로 넘어가면 G R S 비트를 사용해 Round to nearest even(반올림) 해준다.
2022.08.28 - [Computer Science/Computer Architecture] - [Chapter 3. 컴퓨터 연산] IEEE 754 부동소수점 반올림과 근사
여기서 E가 더 작은 쪽을 right shift 하는 이유는
작은 쪽의 소수 부분(F)을 right shift(나누기 2)해야 작은 쪽의 E가 커져서 자릿수 맞춤이 되기 때문이다.
3. F2와 F1을 더해 F3을 만든다.
4. F3을 정규화한다.

5. 정규화된 F3이 표현할 수 없는 비트로 넘어가면 G R S 비트를 사용해 Round to nearest even(반올림) 해준다.
6. F3와 E3를 사용해 부동소수점 표현으로 바꾸어준다.
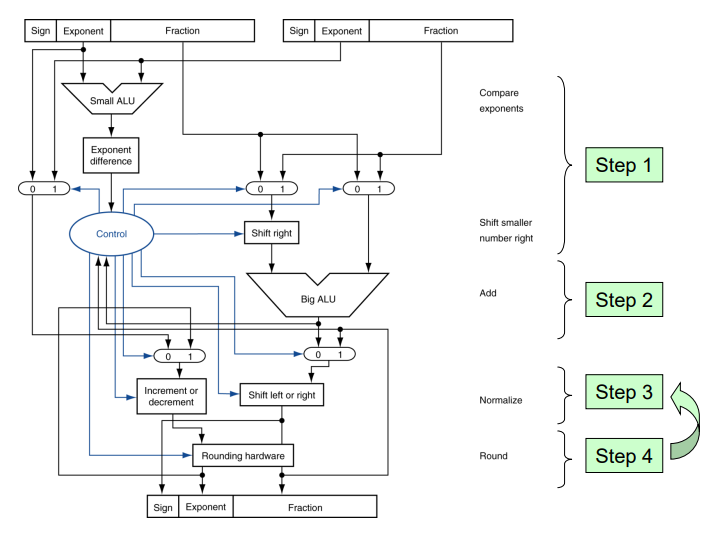
(예시 문제)
0.5 + (-0.4375)를 구해보자.
각각의 수를 정규화하면 다음과 같다.
0.5 = 1.0000 × 2^-1
-0.4375 = -1.1100 × 2^-2
Step 0.
hidden bit은 이미 복구되어 있다.
Step 1.
E1 = -1, E2 = -2
E1 > E2이므로 -1.1100을 right shift 1(E1 - E2) 해준다.
즉, -0.1110 0(G)0(R)0(S) × 2^-1이 되고, G가 0이므로 내림해주어야 한다.
따라서 -0.1110 × 2^-1이 된다.
Step 2.
F3 = F1 + F2 = 1.0000 + (-0.1110) = 0.0001
Step 3.
0.0001 × 2^-1을 정규화하여야 한다.
0.0001 × 2^-1 = 1.000 × 2^-5
Step 4.
GRS 비트는 모두 0이므로 정규화가 완료되었다!
부동소수점 덧셈은 정수 덧셈보다 복잡하기 때문에 더 많은 clock cycle이 소요된다.
부동소수점 곱셈
이번에는 부동소수점으로 표현된 수들의 곱셈은 어떻게 진행되는지 알아보자.
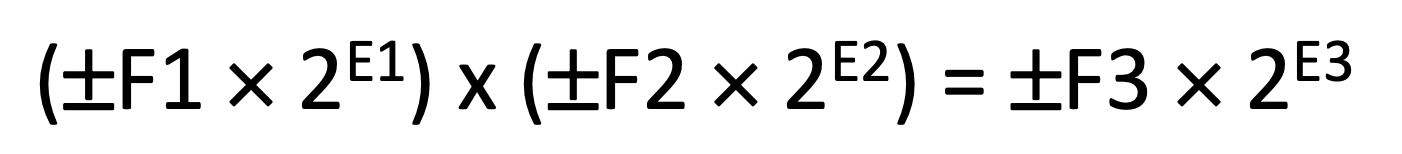
1. F1과 F2의 hidden bit을 복구시킨다.
ex) F1이 011000...000이라면 원래 수는 1.011이다. (hidden bit = 1)
2. 지수 간의 곱을 먼저 진행해준다. 즉, E3 = E1 + E2 - bias이다.
E1 = e1 + bias, E2 = e2 + bias이기 때문에 둘을 더하면 E1 + E2 = e1 + e2 + 2*bias이 된다.
따라서 E1과 E2를 더한 것에서 bias를 빼주어야 하는 것이다. (bias = 127 또는 1023)
또한, MSB가 같은지를 확인하여 부호를 미리 정해준다.
3. F1과 F2를 곱하여 F3를 double precison 형태로 표현해준다.
4. F3를 정규화한다.

5. 정규화된 F3이 표현할 수 없는 비트로 넘어가면 G R S 비트를 사용해 Round to nearest even(반올림) 해준다.
6. E3과 F3을 이용해 부동소수점 표현으로 바꿔준다.
곱셈 하드웨어는 위의 덧셈 하드웨어와 똑같다.
(예시 문제)
0.5 × (-1.1100)를 구해보자.
각각의 수를 정규화하면 다음과 같다.
0.5 = 1.0000 × 2^-1
-0.4375 = -1.1100 × 2^-2
Step 0.
hidden bit은 이미 복구되어 있다.
Step 1.
E3 = E1 + E2 - bias = (-1+127) + (-2+127) - 127 = -3 + 127 = 124
부호는 E1과 E2가 서로 다르기 때문에 음수(-)이다.
Step 2.
1.0000 × 1.1100 = 1.11000000
Step 3.
1.11000000 × 2^-3는 이미 정규화되어 있다.
Step 4.
1.1100 0(G)0(R)0(S)0에서 G가 0이므로 내림해준다.
따라서 1.1100 × 2^-3가 된다!
정규화된 식을 부동소수점 표현으로 변형하는 방법은 아래의 글을 참고하길 바란다.
2022.08.27 - [Computer Science/Computer Architecture] - [Chapter 3. 컴퓨터 연산] 부동소수점
중요한 것은,
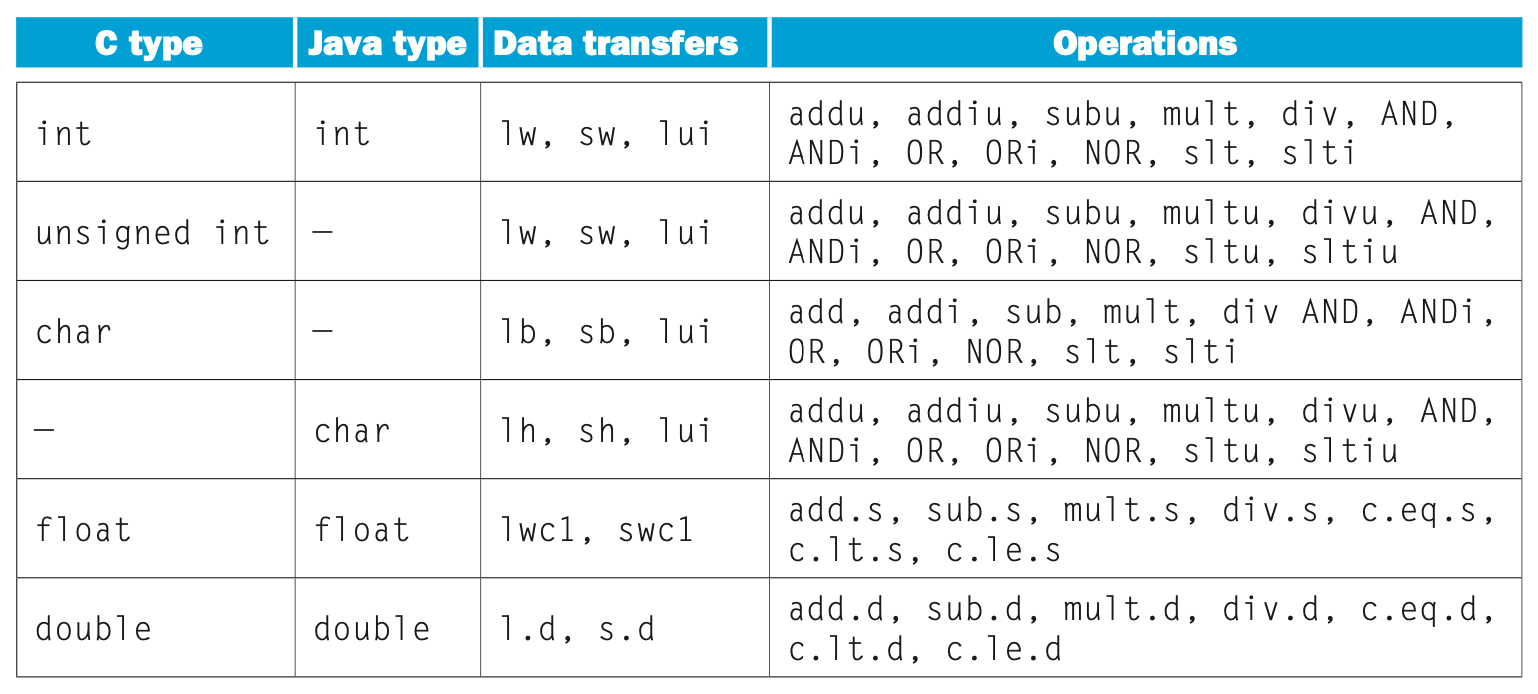
비트 패턴을 통해서 부호있는 정수, 부호없는 정수, 부동소수점 수, 명령어 등을 나타낼 수 있고
무엇을 표현하는가는 워트 내의 비트를 처리하는 명령어에 의해 결정된다는 것이다.
컴퓨터가 표현할 수 있는 수는 크기가 제한되어 있고, 이에 제한된 정밀도를 가지고 있다.
워드로 표현하기에는 너무 큰 수나 너무 작은 수를 계산하게 될 수도 있기 때문에
프로그래머는 이런 제약 조건을 잘 기억하고 여기에 맞추어 프로그램을 적절히 작성해야 한다.
'Computer Science & Engineering > Computer Architecture' 카테고리의 다른 글
| [Chapter 4. 프로세서] 프로세서 구현에 대한 개요 (0) | 2022.08.31 |
|---|---|
| [Chapter 3. 컴퓨터 연산] 연산에 있어서 겪을 수 있는 오류와 함정들 (0) | 2022.08.30 |
| [Chapter 3. 컴퓨터 연산] IEEE 754 부동소수점 반올림과 근사 (1) | 2022.08.28 |
| [Chapter 3. 컴퓨터 연산] 부동소수점 (0) | 2022.08.27 |
| [Chapter 3. 컴퓨터 연산] 나눗셈 (0) | 2022.08.26 |




