봉황대 in CS
[Chapter 3. 컴퓨터 연산] 나눗셈 본문
[Chapter 3. 컴퓨터 연산] 나눗셈
등 긁는 봉황대 2022. 8. 26. 20:37* 본 글은 '컴퓨터 구조 및 설계: 하드웨어/소프트웨어 인터페이스(Computer Organization and Design: The Hardware/Software Interface) 5th edition'의 내용과 2021학년도 1학기에 수강한 '컴퓨터 구조' 과목 강의 내용을 함께 정리하여 작성하였습니다.
나눗셈
나눗셈은 곱셈보다 사용 빈도는 낮지만 훨씬 까다롭다.
0으로 나누기와 같이 수학적으로 유효하지 않은 연산을 요구하기도 한다.
먼저 0과 1로만 이루어진 십진수의 나눗셈, 1001010÷1000을 보자.

나누어지는 수는 피제수(dividend), 피제수를 나누는 수는 제수(devisor)로 부르고,
몫(quotient)이라 불리는 결과와 나머지(remainder)라고 불리는 두 번째 결과가 있다.
피제수 = 몫 × 제수 + 나머지
보통 초등학교에서 배운 나눗셈 방법은 얼마나 큰 수를 뺄 수 있는지를 검사해서 몫의 자리 수를 하나하나 구한다.
위의 십진수 예는 0과 1 만을 사용하도록 선택하였으므로, 제수가 피제수에 얼마나 많이 들어갈 수 있는지 쉽게 알 수 있다.
제수는 피제수에 0번 아니면 1번만 들어간다.
이진수 나눗셈은 이 두 가지 중 한 가지 선택만으로 제한되므로 계산이 간단하다.

초기의 나눗셈 하드웨어
초등학교에서 배운 알고리즘을 그대로 하드웨어로 구현한 것이다.

제수(divisor) 레지스터, ALU, 나머지(remainder) 레지스터는 모두 64비트이고,
몫(quotient) 레지스터만이 32비트이다.
제수는 64비트 제수 레지스터의 왼쪽 절반에 넣어지고,
나머지 레지스터는 피제수로 초기화된다.
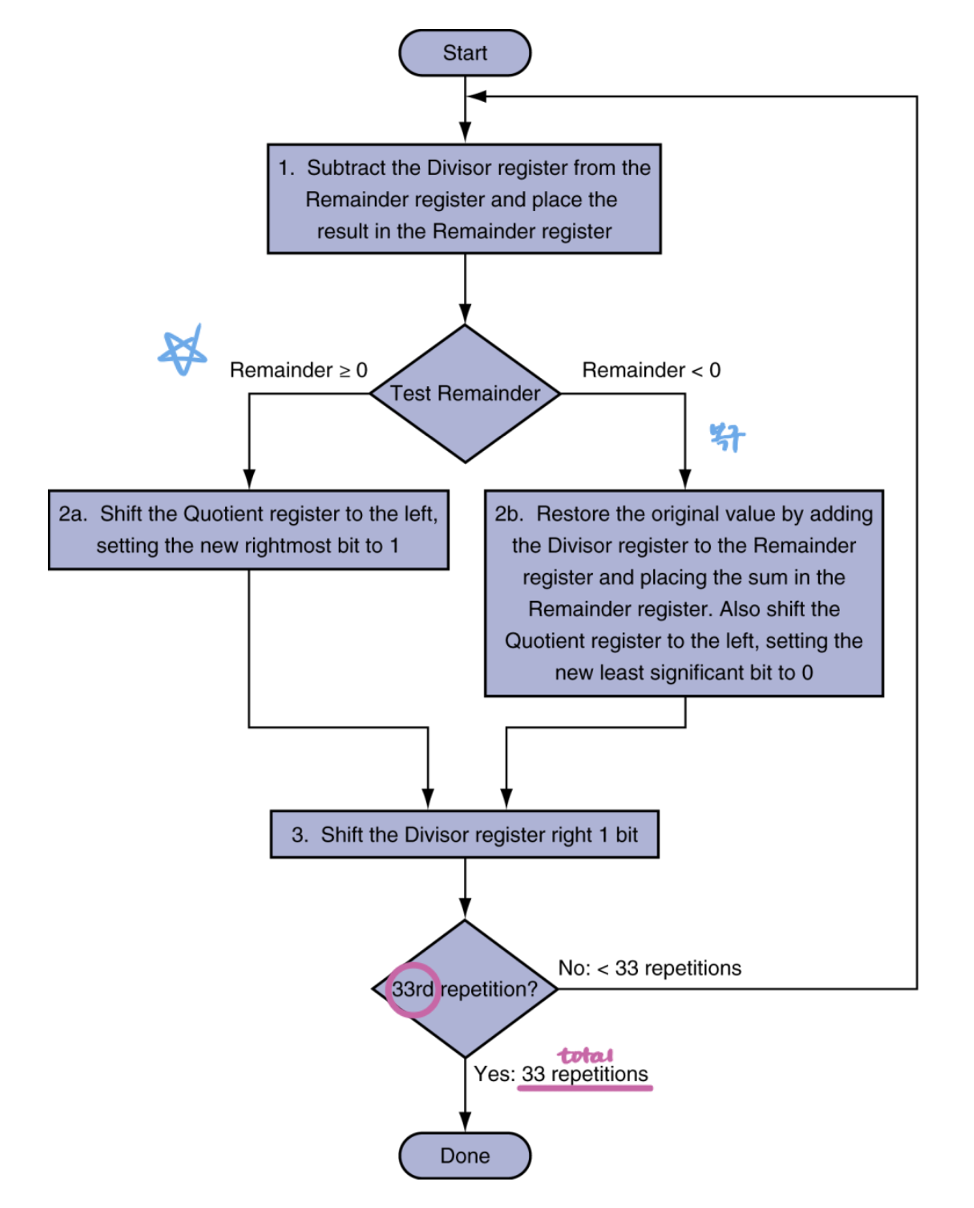
[ 단계 1 ]
컴퓨터는 제수가 피제수보다 작다는 것을 먼저 알 만큼 똑똑하지 않으므로, 일단 나머지 레지스터에서 제수를 빼야 한다.
[ 단계 2 ]
나머지 레지스터에서 제수를 뺀 결과가 양수라면 제수는 피제수와 같거나 더 작다는 것이므로 몫에 1을 넣는다.
결과가 음수라면 제수를 나머지 레지스터에 다시 더해서 원래의 값을 회복한다.
이러한 복구 연산이 존재하기 때문에 나누기 연산은 복잡하다.
[ 단계 3 ]
제수 레지스터를 오른쪽으로 한 비트씩 자리이동(shift right)시킨다.
이는 다음번 반복의 계산을 위해 피제수에 맞추어 제수를 정렬시키기 위함이다.
최종 결과를 얻기 위해서는 이 세 단계를 33번 반복해야 한다.
제수 레지스터에는 사용되지 않는 부분이 존재하는데,
이 부분을 개선하는 것을 통해 덧셈기와 레지스터의 크기를 절반으로 줄일 수 있다.
개선된 나눗셈 하드웨어
제수(divisor) 레지스터, ALU, 몫(quotient) 레지스터는 모두 32비트이며,
나머지(remainder) 레지스터만이 64비트로 남아있다.
몫 레지스터는 나머지 레지스터의 오른쪽 절반에 결합되었다.

초기의 나눗셈 하드웨어에서 자리이동된 제수 레지스터는 가만히 있고,
나머지 레지스터를 왼쪽으로 자리이동(shift left)한다.
예시로 0111(7)÷0010(2)의 계산을 적어놓았으니, 찬찬히 보면서 과정을 이해하길 바란다.
지금까지는 양수만을 다뤄왔다.
부호있는 수의 나눗셈은 어떻게 해야할까?
곱셈에서와 같이, 간단한 방법은 제수와 피제수의 부호를 기억하고
전부 양수로 변환하여 나눗셈을 실행한 다음, 제수와 피제수의 부호가 달랐을 경우 몫을 음수화하는 것이다.
앞서 설명한 곱셈 하드웨어와 나눗셈 하드웨어가 똑같다는 것을 볼 수 있다.
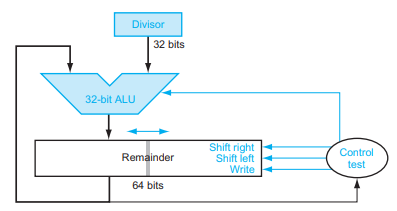
즉, 똑같은 순차 하드웨어가 곱셈과 나눗셈 모두에 이용될 수 있다는 것이다.
왼쪽이나 오른쪽으로 자리이동될 수 있는 64비트 레지스터와
덧셈과 뺄셈을 할 수 있는 32비트 ALU만 있으면 된다.
MIPS는 곱셈과 나눗셈용 64비트 레지스터로 32비트 hi와 lo 레지스터를 사용한다.
MIPS 나눗셈 명령어
MIPS에서는 부호있는 정수와 부호없는 정수를 모두 다루기 위해
두 개의 명령어 div(divide)와 divu(divide unsigned)를 지원한다.
div $s0, $s1 # lo = $s0 / $s1
# hi = $s0 mod $s1나눗셈 명령이 완료된 뒤 hi는 나머지를, lo는 몫을 갖는다.
MIPS 어셈블러는 범용 레지스터 세 개를 사용하는 나누기 의사명령어 mflo와 mfhi를 제공한다.
mfhi rd
mflo rd이들을 통해 원하는 결과를 범용 레지스터에 넣는다.
'Computer Science & Engineering > Computer Architecture' 카테고리의 다른 글
| [Chapter 3. 컴퓨터 연산] IEEE 754 부동소수점 반올림과 근사 (1) | 2022.08.28 |
|---|---|
| [Chapter 3. 컴퓨터 연산] 부동소수점 (0) | 2022.08.27 |
| [Chapter 3. 컴퓨터 연산] 곱셈 (0) | 2022.08.25 |
| [Chapter 3. 컴퓨터 연산] 덧셈과 뺄셈, 오버플로우 탐지와 처리 (0) | 2022.08.24 |
| [Chapter 2. 명령어: 컴퓨터 언어] 프로그램 번역 과정과 동적 링크 라이브러리 (1) | 2022.08.23 |




