| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 컴퓨터구조
- 부동소수점
- concurrency
- 스케줄링
- 알고리즘
- 페이지 부재율
- local cache
- 단편화
- mips
- 인터럽트
- 세마포어
- 백준
- garbage collection
- 페이징
- 페이지 대치
- fork()
- 스레드
- PYTHON
- 우선순위
- ALU
- redis
- 가상 메모리
- 프로세스
- mutex
- 운영체제
- gc
- Algorithm
- 교착상태
- 기아 상태
- BOJ
- Today
- Total
봉황대 in CS
Separation or Not: On Handing Out-of-Order Time-Series Data in Leveled LSM-Tree 본문
Separation or Not: On Handing Out-of-Order Time-Series Data in Leveled LSM-Tree
등 긁는 봉황대 2023. 9. 7. 17:052022 IEEE 38th IDCE
Separation or Not: On Handing Out-of-Order Time-Series Data in Leveled LSM-Tree
LSM-Tree is widely adopted for storing time-series data in Internet of Things. According to conventional policy (denoted by <tex xmlns:mml="http://www.w3.org/1998/Math/MathML" xmlns:xlink="http://www.w3.org/1999/xlink">$\pi_{c}$</tex> ), when writing, the
ieeexplore.ieee.org
Apache IoTDB
- leveled LSM-Tree based, high-performance data engine tailored for time-series data
- separation policy (πs, MemTable : 1/2 C_seq, 1/2 C_nonseq)
C_seq : in-order MemTable
C_nonseq : out-of-order MemTable
Two policies on MemTable
πc : conventional policy
- C_0 : 기존 LSM-Tree의 방식과 동일 (하나의 MemTable)
πs : separation policy
- C_seq : stores in-order data points
- C_nonseq : stores out-of-order data pionts

하나의 append-only Skiplist → overhead가 많이 큰가??
Separation Policy
- advantage : only requires compaction when C_nonseq is full
- problem : if there is only a few out-of-order data points, WA will increase than using conventional policy

Write amplification, WA
(data가 disk에 실제로 write 된 횟수) / (user가 data write을 요청한 횟수)
Time-series data points
p = <tg, ta, v>
tg : timestamp when the data point is generated
unique → identifies a specific data point
ta : timestamp when the data point arrives in the database
v : value→ SST’s entries are sorted by generation time
Time-series S = {p1, p2, ... , pi, ...}
: collection of time-series data pointstime interval to generate data points : Δt
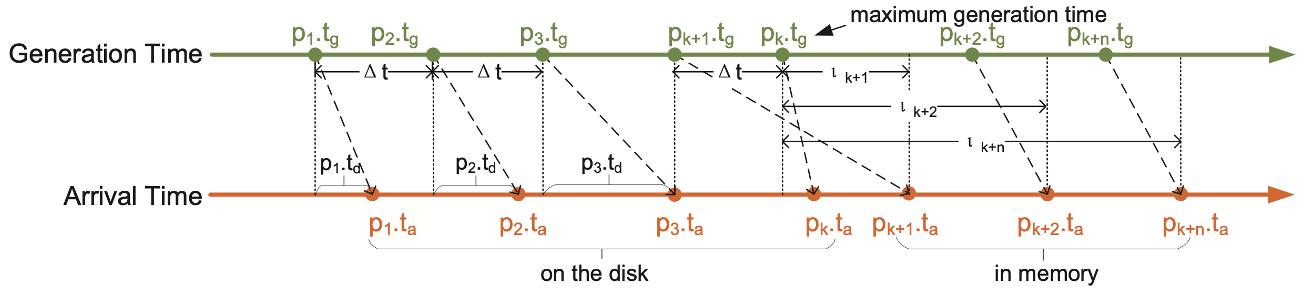
Delay
p.td = p.ta - p.tgin terms of generation time, time-series data are unordered because there are various delays
caused by clock skew, network delays, system recovery from failure, etc.
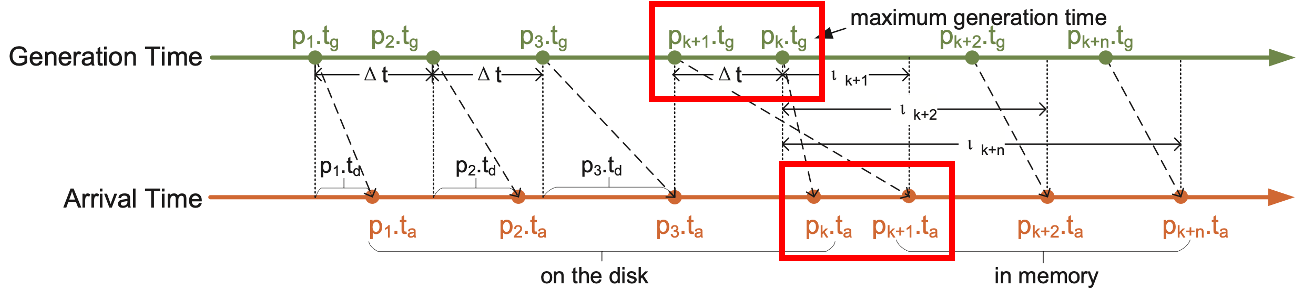
LAST(R)
- level L1 (notated in this paper) means disk level 0 = run = R
- LAST(R) : the entry with the latest generation time in R
즉, disk에 저장된 entry 중 generation time이 가장 느린(가장 최근에 생성된) data point를 말한다.
In-order data points
if new-arriving data point is generated later than all of the data points on the disk
p.tg > LAST(R).tg
Out-of-order data points
if new-arriving data point is generated earlier than all of the data points on the disk
p.tg < LAST(R).tg
Factors affecting WA
1. MemTable policy
choosing the policy should be dependent on the intensity of disorder of the writing workload
Experiments
: 선택한 정책과 workload 상황에 따라서 WA와 query performance가 어떻게 달라지는가?
[ datasets ]
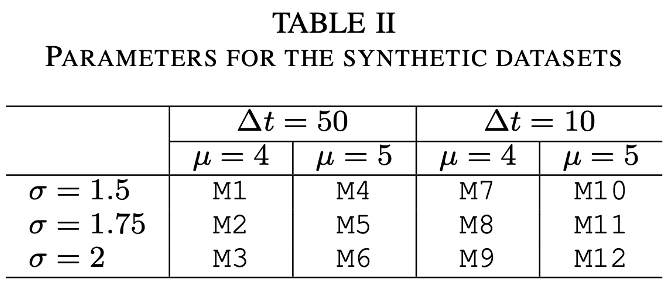
µ : 평균
µ가 증가할수록 delay의 정도가 커진다는 것이다.
σ : 표준편차
σ가 증가할수록 delay의 정도가 많이 퍼져있다는 것이다. 즉, 제각각이다.
[ WA ]
WA.πs < WA.πc
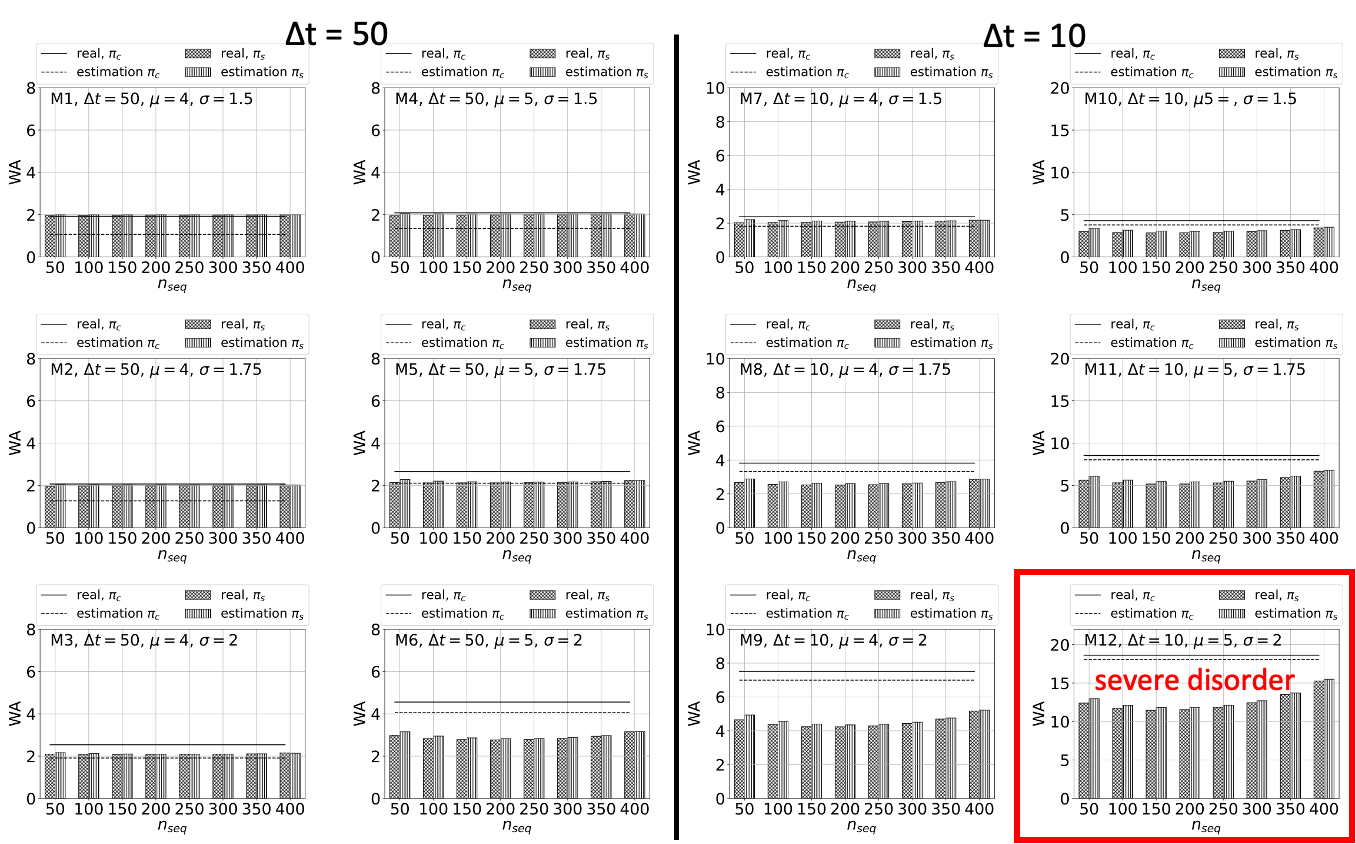
[ Query performance ]
πc is better than πs
why?
- in πs, the SSTables included in the query range are fewer,
- but as the size decreases, the files to read increases
1. recent data query
select *
from TS
where time > (max_time - window)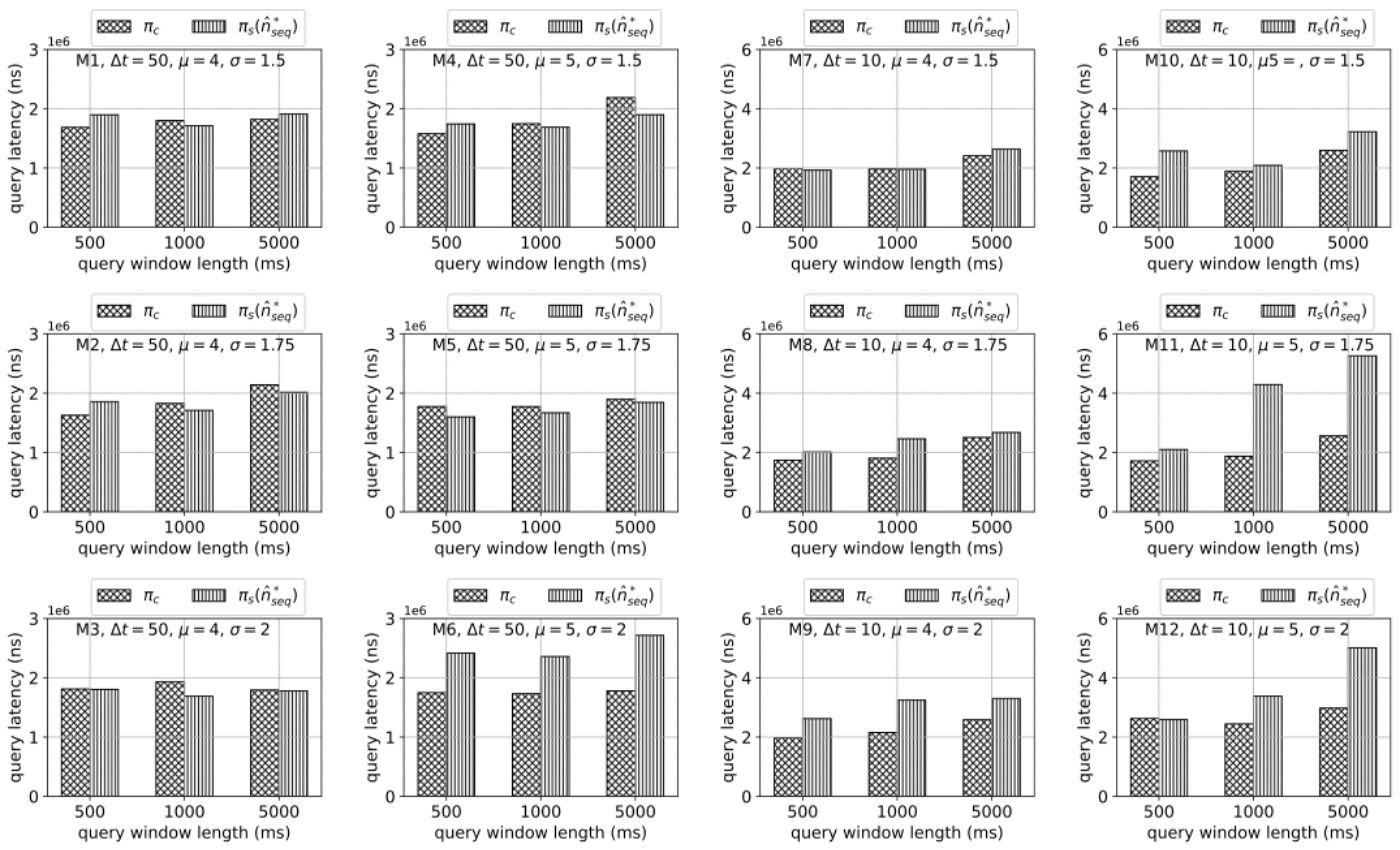
2. historical data query
select *
from TS
where time > rand_value and time < rand_value + window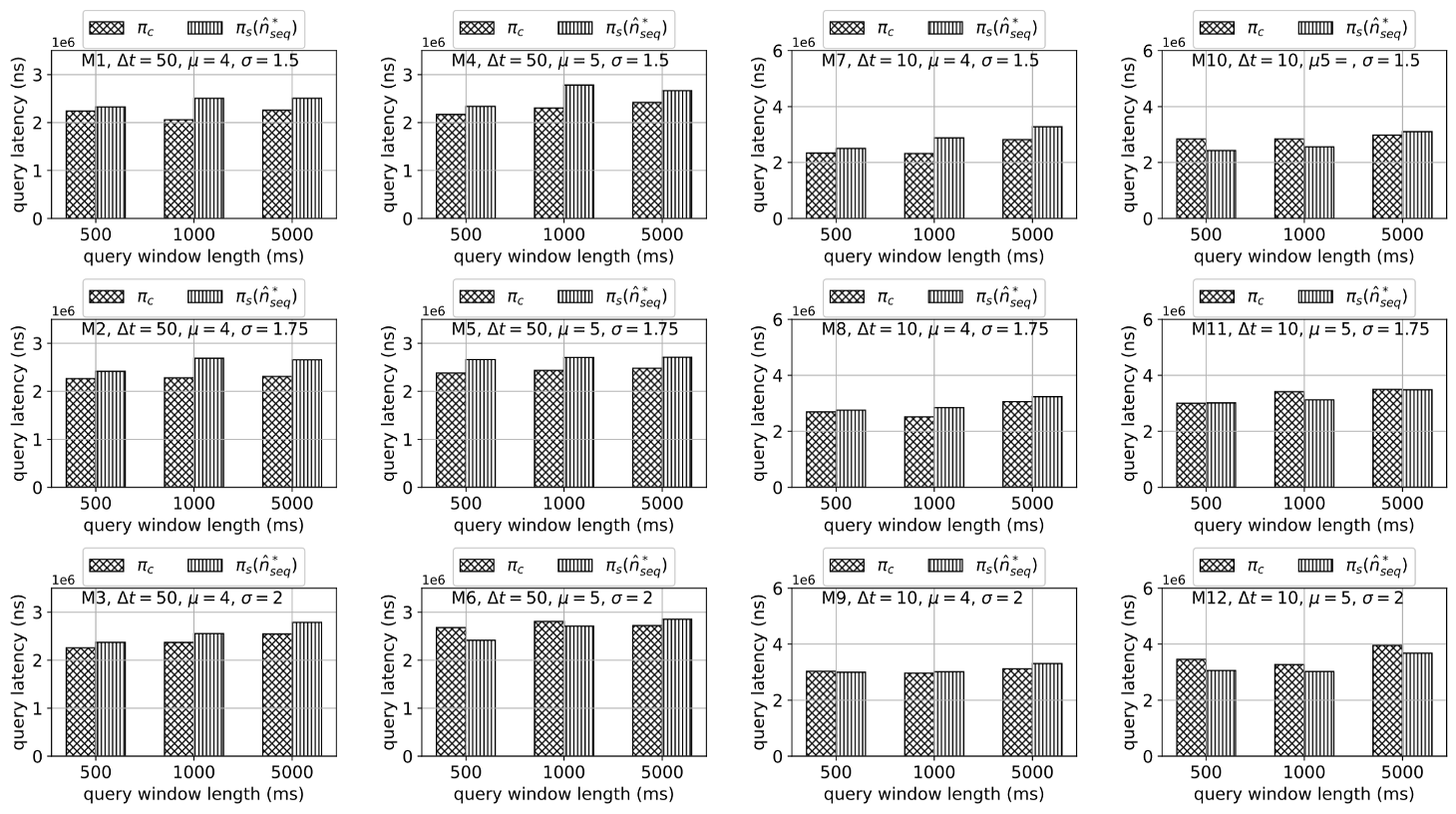
2. Capacity of C_nonseq
the total MemTable capacity is not tunable (n_0 = n_seq + n_nonseq)
if C_nonseq is too small,
C_nonseq will fill more often, causing frequent compaction
if C_nonseq is too large,
C_seq will fill more often, causing more data points treated as out of order
(because it updates the max generation time on the disk frequently)
Separation or not
main idea : predict the WA under two policies & select the best policy at that point
1. What is the WA under πc?
2-1. Under πs, how does WA change with different capacities of C_seq?
2-2. What is the minimum WA in this case? (minimum WA under πs)

πs(n*_seq)
means the separation policy, where the capacity of C_seq is set to be n*_seq
How can we predict the WAs??
: by predicting the number of subsequent data points
Subsequent data points
p : on-disk data point
C_0 : in-memory MemTable
if there is any data point q ∈ C_0, p.tg > q.tg,
then p is a subsequent data point of C_0즉, 현재 MemTable에서 가지고 있는 어떤 key q가 disk에 저장되어 있는 어떤 key p보다 늦게 생성된 놈일 때(→ q is out-of-order data point), p를 subsequent data point라고 부른다.
During compaction, any SSTable containing subsequent data points should be rewritten
rc : WA under πc
- n : the capactiy of C_0
- ζ(n) : the expectation of the number of subsequent data points
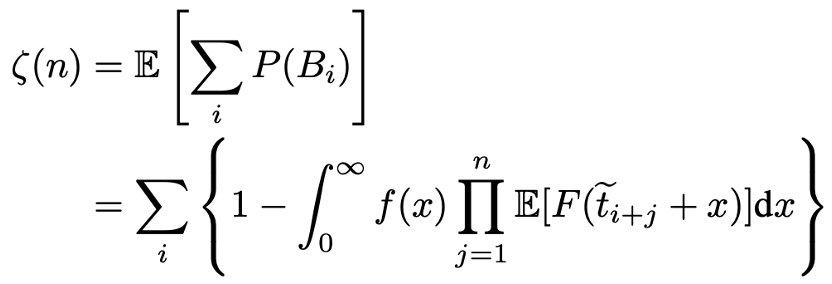
(P(Bi) : the probability of being a subsequent data point)
rs : WA under πs

- N_cur(n_seq) : number of data points to rewrite = 전체 - out-of-order - last-flushed SSTable(→ 왜 빼는가???)
- n'_seq : number of data points in the last-flushed SSTable
- unit : a phase (= C_nonseq의 주기)
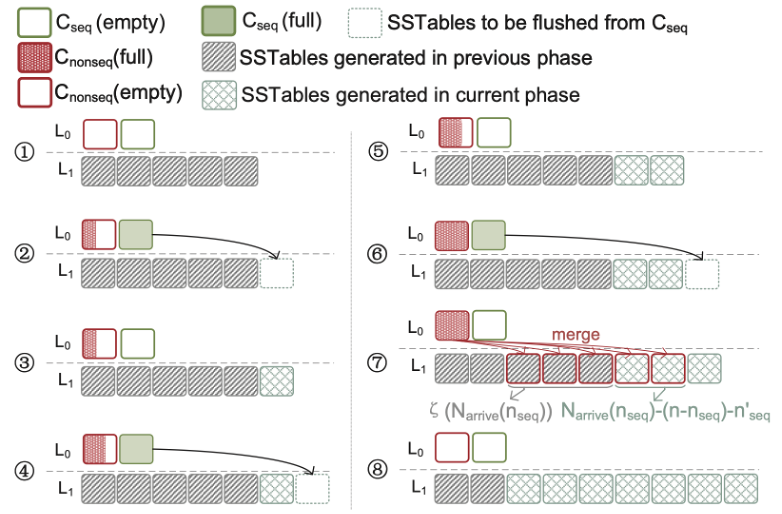
위 수식에서 (n-n_seq+n'_seq) / N_arrive(n_seq) 부분은 이해하지 못했다....
(N_cur를 통해서 정리된 부분인 것 같은데 왜 저렇게 이어지는지 모르겠음)
Experiment - correctness
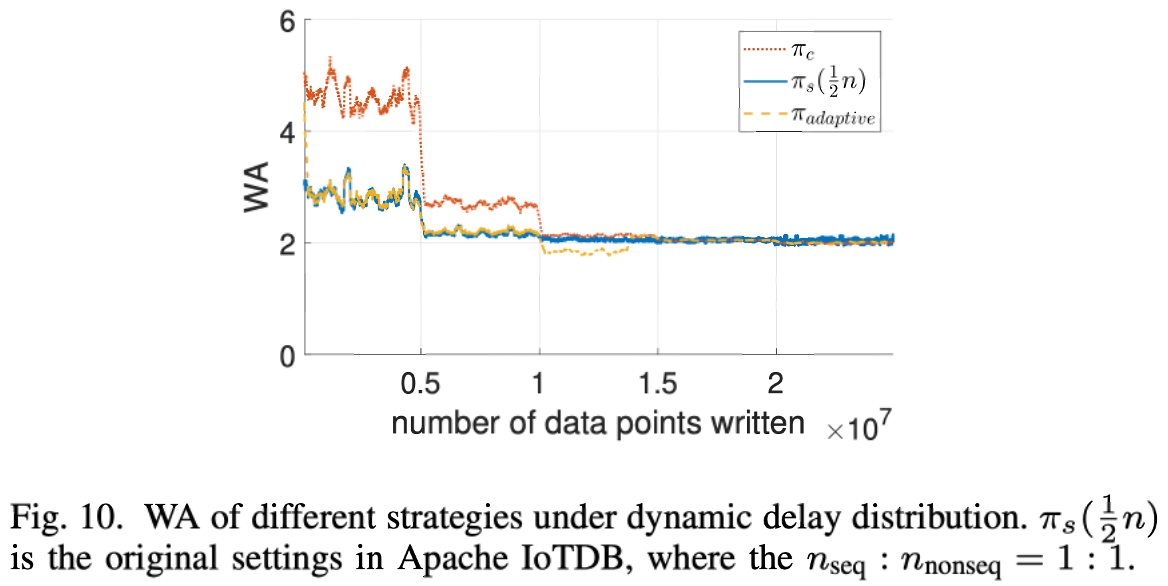
→ the model can accurately predict the WA & choose the better policy so that the WA is reduced
'Database' 카테고리의 다른 글
| [Oracle] Database Physical & Logical Storage Structures (4) | 2024.07.02 |
|---|---|
| [Concurrency Control] Optimistic Version Locking (2) | 2024.06.10 |
| Bottom-Up Build of a B+-Tree (Bulk-Loading) (4) | 2024.01.01 |
| XIndex: A Scalable Learned Index for Multicore Data Storage (2) | 2023.10.03 |
| LSM-Tree에 대한 고찰 (4) | 2023.08.17 |



