[알고리즘] 분할 정복, Divide-and-Conquer
정렬 알고리즘들에 대하여 알아보던 중, 합병 정렬(merge sort)과 퀵 정렬(quick sort)이 분할 정복 알고리즘 중 하나임을 깨닫고
먼저 분할 정복에 대해 정리하기 위하여 이 글을 작성한다.
분할 정복 (Divide-and-Conquer)
'쪼개서 풀고 합하기'
: 문제를 잘게 쪼개는 분할(Divide) + 문제를 풀어서 합하는 정복(Conquer)
분할 정복이란,
그대로 해결할 수 없는 문제를 작은 문제로 분할하여 해결하는 방법이다.
즉, 문제를 작은 2개의 문제로 분리한 후 각각을 해결한 다음, 그 결과들을 모아서 원래의 문제를 해결하는 전략을 말한다.
(Top-down, 하향식 접근법)
조건
1.
문제를 쪼개 나가는 과정에서, 큰 문제와 작은 문제의 구조가 동일하거나 비슷해야 한다.
= 큰 문제에서 적용되는 해결법이 작은 문제에서 동일하게 적용된다.
2.
쪼개진 문제들 사이에는 상관관계가 없어야 한다.
= 쪼개진 문제들이 풀이 과정에서 서로 영향을 주지 않아야 한다.
재귀 함수의 이용
위의 조건을 보면 재귀 함수와 잘 맞음을 볼 수 있다.
따라서 분할 정복을 위해서는 재귀 함수를 이용하게 되는데,
일반 재귀 호출과는 다르게 문제를 거의 같은 크기의 부분 문제로 나누어서 진행한다. (조건 1)
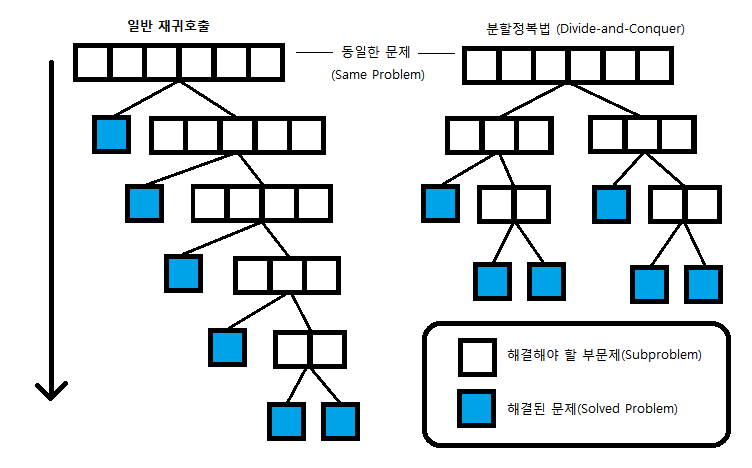
재귀 함수를 선언할 때에는 아래와 같이 두 부분으로 나누어서 구현해야 한다.
1. 큰 문제를 작은 문제로 재귀적으로 쪼개는 부분
2. 문제를 최소 단위로 쪼갰을 경우 문제를 풀이하는 부분
과정
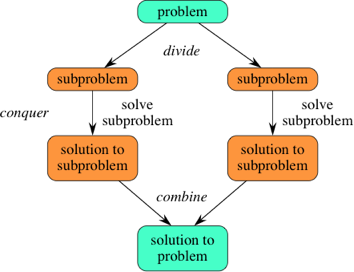
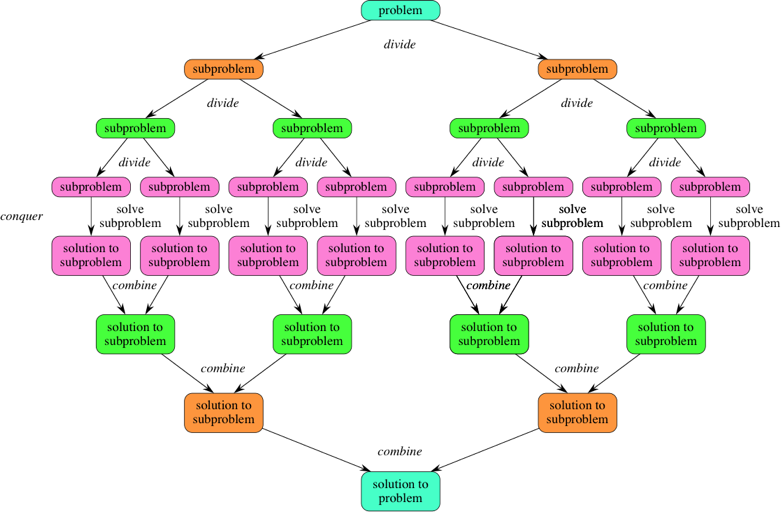
1. 분할 (divide) : 원래 문제를 분할하여 비슷한 유형의 더 작은 하위 문제들로 나눔
2. 정복 (conquer) : 하위 문제 각각을 재귀적으로 해결
3. 합치기 (combine) : 하위 문제들의 답을 합쳐서 원래 문제를 해결
정렬 알고리즘 시간복잡도 비교 (병합 정렬, 퀵 정렬)
분할 정복을 사용하는 정렬 알고리즘에는 병합 정렬(Merge Sort)과 퀵 정렬(빠른 정렬, Quick Sort)이 있다.
그 외의 여러 정렬들(삽입 정렬, 선택 정렬, 버블 정렬, 힙 정렬 등)과 시간복잡도를 비교해보면 다음과 같다.
| Best | Avg | Worst | Run-time (정수 60,000개) |
|
| 삽입 정렬 (Insertion Sort) |
N | N^2 | N^2 | 7.438 sec |
| 선택 정렬 (Selection Sort) |
N^2 | N^2 | N^2 | 10.842 sec |
| 버블 정렬 (Bubble Sort) |
N^2 | N^2 | N^2 | 22.894 sec |
| 힙 정렬 (Heap Sort) |
N log2(N) | N log2(N) | N log2(N) | 0.034 sec |
| 병합 정렬 (Merge Sort) |
N log2(N) | N log2(N) | N log2(N) | 0.026 sec |
| 퀵 정렬 (Quick Sort) |
N log2(N) | N log2(N) | N^2 | 0.014 sec |

즉, 분할 정복을 사용하는 정렬 알고리즘들이 나머지들보다 훨씬 효율적임을 볼 수 있다.
구현이 간단하지만 비효율적인 방법 : 삽입 정렬, 선택 정렬, 버블 정렬
구현이 복잡하지만 효율적인 방법 : 힙 정렬, 병합 정렬, 퀵 정렬
문제 추천
1992번: 쿼드트리
첫째 줄에는 영상의 크기를 나타내는 숫자 N 이 주어진다. N 은 언제나 2의 제곱수로 주어지며, 1 ≤ N ≤ 64의 범위를 가진다. 두 번째 줄부터는 길이 N의 문자열이 N개 들어온다. 각 문자열은 0 또
www.acmicpc.net